Two Important Things to be Considered

Now you have come this far so we would like to consider two more things before going on to take the quiz, or have a cup of coffee and a doughnut.

Risk-reward Ratio

The first important thing you need to consider is the risk-reward ratio.

This refers to how much we are risking and willing to make on each trade. On the examples before, we used a 3:1, meaning that for every dollar you are risking in any trade, you are willing to make three dollars. But we will talk about this in the following lesson.

Expectation

The second thing you should have in mind is the expectation of a given system. MM makes sure you are going to be able to trade tomorrow and allows your profits to grow geometrically. It is not a magic wand though so it cannot turn a losing system into a winning system (or a system with a negative expectancy into a system with a positive expectancy)

The formula to calculate the expectancy of any system is:

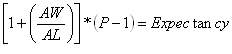
[Image 1]

where,

AW = Average winning trade in terms of $

AL = Average losing trade in terms of $

P = is the probability to win any given trade.

Take for instance the following system

System based on MA crossovers. In a sample of 100 trades, the following information is obtained:

Number of trades = 100
Winning trades = 62
Losing trades = 38
Average winning trade = $800
Average losing trade = $600

The expectancy of this system is as follows:

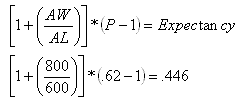
[Image 2]

This system has a positive expectancy: the greater the number, the better the system is.

A negative result would mean that the system has a negative expectancy and no MM can turn this system into a winning system, the only thing it could do for the system is to limit the losses.